查找算法是什么？查找算法如何实现

查找算法也可以叫搜索算法。查找算法就是从一个有序数列中找出一个特定的数，常用于判断某个数是否在数列中，或者某个数在数列中的位置。在计算机应用中，查找是常用的基本运算，是算法的重要组成部分。下面来看算法中的顺序查找、二分查找、插值查找和分块查找，介绍他们的实现方法。

顺序查找

顺序查找(也被称为线性查找)是最简单、最直接的查找算法。顾名思义，顺序查找就是将数列从头到尾按照顺序查找一遍，是最容易理解的算法。

举例：我们要从下面数列中找到“1”这个元素。

我们要从下面数列中找到“1”这个元素，从第一个元素开始遍历，逐一比较。

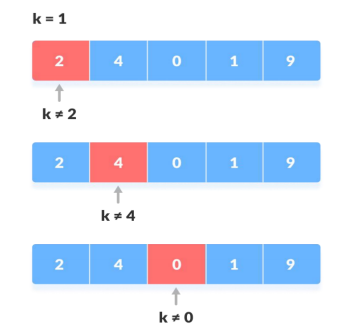
我们要从下面数列中找到“1”这个元素，从第一个元素开始遍历，逐一比较，直到找到(或遍历完成)为止。

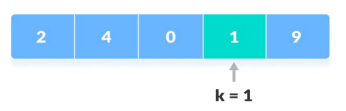
def sequentialSearch(ilist, key):
    iLen = len(iList)
    for i in range(iLen):
        if ilist[i] == key:
          return i
    return -1

顺查找的时间复杂度O(n)，空间复杂度0(1)。

二分查找

(Binary Search)是应用在有序数据中的，十分高效的查找算法。如果数据是无序的，我们先要将数据从小到大排序。其原理是比较待查数据与数组中值的数据的大小，如果等于中间值则直接返回，如果大于中间值，就只在后半部分查找，如果小于中间值，就在前半部分查找，如此往复，直到找到数据，或剩下一个元素。

二分查找代码实现

def binary_search(iList, key):
    iLen = len(iList)
    left = 0
    right = iLen -1
    while right - left > 1:
        mid = (left + right) // 2
        if key < ilist[mid]:
          right = mid
        elif key > ilist[mid]:
            left = mid
        else:
          return mid
    if key == iList[left]:
        return left
    elif key == ilist[right]:
        return right
    else:
      return -1

二分查找的时间复杂度是o(logn)

①在n个元素中寻找→②在n/2个元素中寻找→③在n/4个元素中寻找….在1个元素中寻找

n经过几次“2”=1→log2n=0(logn)

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束。如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。

如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

二分查找的时间复杂度：0(logn)

插值查找

插值查找(lnterpolation Search)是对实例的二分查找的改进，其应用场景是排序数组中的值是均匀分布的。二分查找总是到中间元素做左右划分，而插值搜索会根据正在搜索的Key的大小来确定划分的位置例如，如果Key更接近最后一个元素，则插值搜索会从后半部分开始进行数据划分。

Mid =L + (R-L) x (target–data[L]) / data[R]-data[L]

插值查找举例：

Mid = L +(R-L)(target- data[L]) / data[R]-data[L]= 0+(7-0) ×(11-1)÷(14-1) =7× 10÷13 = 5.38

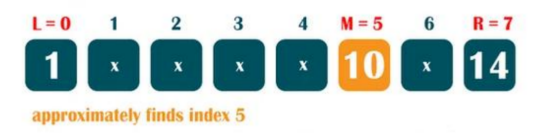
插值查找代码

def interpolation_search(ilist, key):
    iLen = len(iList)
    left = 0
    right = iLen - 1

    while right - left > 1:
        mid = left + (key -iList[left]) * (right - left) // (iList[right] - iList[left])
        if mid == left:
            mid +=1  # 当ilist[right]和ilist[left]相差太大,有可能导致mid一直等于left陷入死循环
        if key < iList[mid]:
            right = mid
        elif key > ilist[mid]:
            left = mid
        else:
          return mid
    if key == ilist[left]:
        return left
    elif key == iList[right]:
        return right
    else:
        return -1

二分查找的改进，适合均匀分布的有序数组插值查找算法的复杂度是0(loglogn)。

分块查找

分块查找和以上几种查找方式有所不同：顺序查找的数列是可以无序的;二分法查找和插入查找的数列必须是有序的;分块查找介于两者之间，需要块有序，元素可以无序。

分块查找，先按照一定的取值范围将数列分成数块。块内的元素是可以无序的，但块必须是有序的。所谓块有序，就是处于后面位置的块中的最小元素都要比前面位置块中的最大元素大。

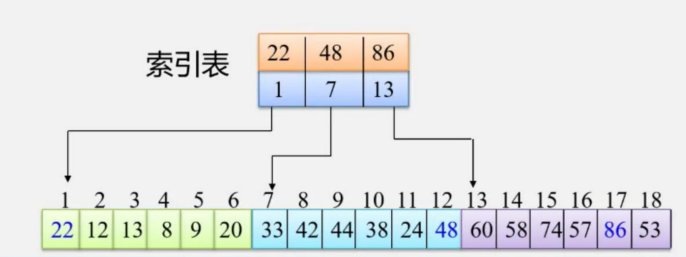
分块查找查找过程：

①确定待查记录所在块(顺序或折半查找)

②在块内查找(顺序查找)

iList = randomList(20)
indexList = [[250, 0], [500, 0], [750, 0], [1000, 0]]

def divideBlock():
    global ilist, indexlist
    sortList = []
    for key in indexList:
        subList = [i for iin iList if i<key[e]]#列表推导，小于key[e]的单独分块
        key[1] = len(subList)
        sortList += subList
        iList=list（set（iList）- set（subList））#过滤掉已经加入到subList中的元素
    ilist = sortlist
    return indexList

def blockSearch(iList, key, indexList):
    left = 0 #搜索数列的起始点索引
    right=e#搜索数列的终点索引
    for indexInfo in indexList:
        if(left+right)<len(iList):
          left += right
        right += indexInfo[1]
        if key < indexInfo[0]:
            break
    for i in range(left, right):
        if key == ilist[i]:
            return i
    return -1